Estimation of Average Speeds
So, in further speculation of a car racing a bicycle, I have graphed out what I know so far.
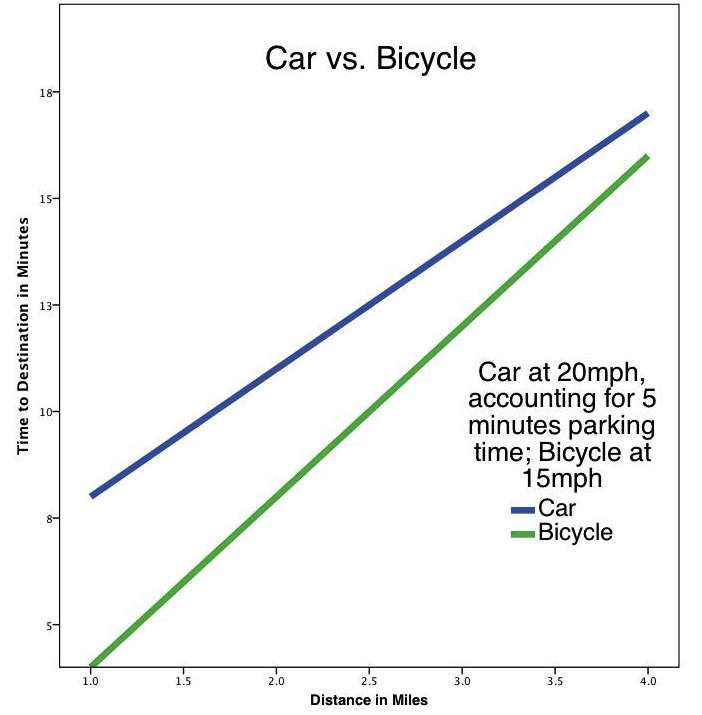
Assuming the car is going 20 mph, and the bike is going 15 mph, the car will win every time. Obviously, we don’t need any math to figure out that 20 mph > 15mph, but that’s not the question I’m interested in. The real question is “who gets there first?”, so I estimated about 5 extra minutes for parking, walking to the car, and walking from the parked car.
For out race, we’re doing a common city trip, which is typically less than 4 miles.
They y-axis is time, so the faster vehicle is the lower line (bike, in this case). It is obvious that the lines will cross eventually, maybe around 5 miles, but for the majority of city drives, the bicycle is actually faster.
Before anyone gets upset: yes I know that cars can go faster than 20 mph, but this is average speed. So, when you kick it up and drive 60 mph down Broadway, for 10 seconds, and screech to a halt in front of a red light, and wait for 30 seconds, your average speed is 17 mph. Meanwhile, the bicycle is a more steady pace, and doesn’t need to stop as often or for as long. Some might say that I am underestimating the car, but I’d say that I am actually overestimating the car’s speed in a city.
I might be overestimating the bicycle as well. I have overall averages of my cycling down this route, but I wasn’t timing myself with a real test in mind. Then again, I wasn’t racing anyone either.
Personally, I’d like to test this. Maybe someone with resources or social clout could help me out (Shane? Interested? Eh?).
Both the driver and the cyclist would have to start form home, so we can add in the extra time for the driver. The driver would have to walk to his car, drive, then park, then walk from the parking spot. I think that this would provide more external validity, so that we could generalize to the larger population of drivers.
Anyone want to race a car? Anyone was to drive against a cyclist?
 4 Comments
4 Comments
i would race any car in boston during rush hour and whooop they bottoms! for serious. I think you are being far too generous with your speed for the car, with all the red lights, traffic, etc. they are going to be way slower.
hey we do this race at Bikes Not Bombs in the Youth Program. Bikes win everytime. We usually race from BNB Hub in JP to JP Licks on Newbury Street. Cars are at a disadvantage due to traffic and bikes are at an advantage due to the bike path…but yeah…it seemed like a pretty easy race to organize. Just get a couple of people and do it 🙂
No WAY! The cars will KILL the biker. You guys don’t know anything. In the post right before this, the traffic lets up around 10 hills, and they’re going at yellow speed. It’s great that BNB does this in JP, but it is a different story here. Broadway’s traffic isn’t always bad and typically lets up around winter hill. Yeah, so any bikers with a 3 minute lead all of a sudden have to climb a san franciscan hill, WHILE all the traffic dissapates around them. No way a biker would win that race.
Alfie –
At morning rush-hour I promise I would beat a car from my house near Tufts to Charlestown, and that includes riding up the Main Street side of Winter Hill. A car may climb the hill faster, but they have to wait two (or more) light cycles at the top. As I mentioned in my comment to the previous post, I believe Sullivan Square will be the end of the car’s chances.